Stock screening using eight criteria
criteria.RmdThe goal of this notebook is to demonstrate stock screening using the following eight criteria:
- PE ratio < 22
- Return on invested capital > 9%
- Revenue growth
- Net income growth
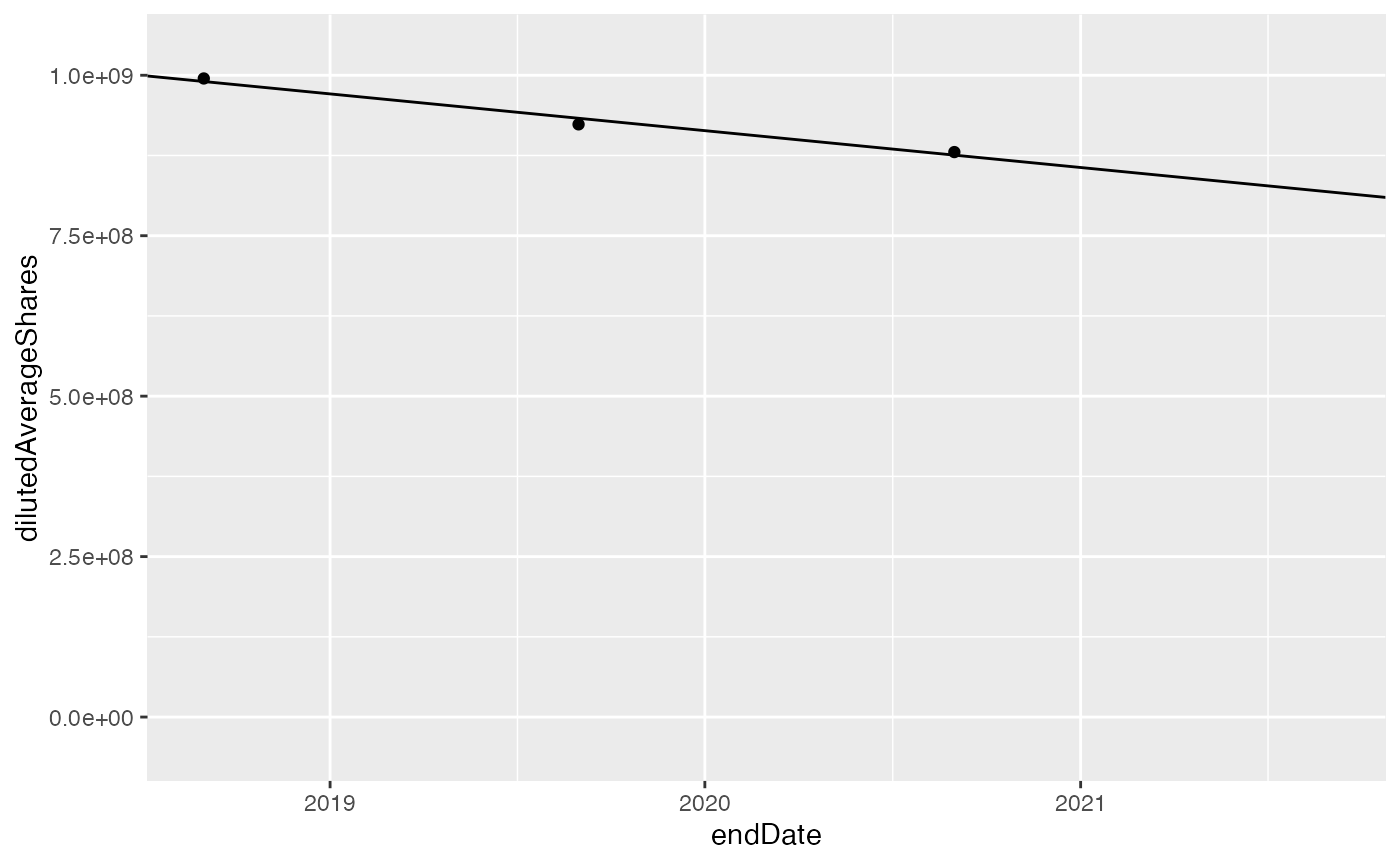
- Shares outstanding decreasing or even
- Long term liabilities / 5 year free cash flow < 5
- Free cash flow growth
- Price to free cash flow < 20
Let’s do this for Best Buy, ticker BBY.
ticker <- "WBA"
fin <- yahoo_financials(ticker)
fin_web <- yahoo_financials_web(ticker)
fin_web## # A tibble: 4 × 5
## endDate basicEps dilutedEps basicAverageShares dilutedAverageShar…
## <dttm> <dbl> <dbl> <dbl> <dbl>
## 1 2021-08-31 00:00:00 NA NA NA NA
## 2 2020-08-31 00:00:00 0.52 0.52 879400000 880300000
## 3 2019-08-31 00:00:00 4.32 4.31 921500000 923500000
## 4 2018-08-31 00:00:00 5.07 5.05 991000000 995000000PE ratio < 22
For the trailing PE ratio, use current price and the EPS history from yahoo_financials_web():
price <- yahoo_history(ticker, interval = "1d", days = 1, end_date = Sys.time()) %>%
arrange(desc(date)) %>%
head(1)
price## # A tibble: 1 × 8
## date open high low close adjusted_close volume symbol
## <dttm> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 2021-12-16 00:00:00 48.5 49.9 48.5 49.6 49.6 1629754 WBA
pe_ratio <- price$open / mean(fin_web$dilutedEps, na.rm = TRUE)This gives us a mean PE ratio of 14.73.
ggplot() +
geom_bar(aes(x = fin$endDate, y = fin_web$dilutedEps), stat = "identity", fill = "#33658A", width = as.numeric(days(100))) +
xlab("date") + ylab("Earnings per share")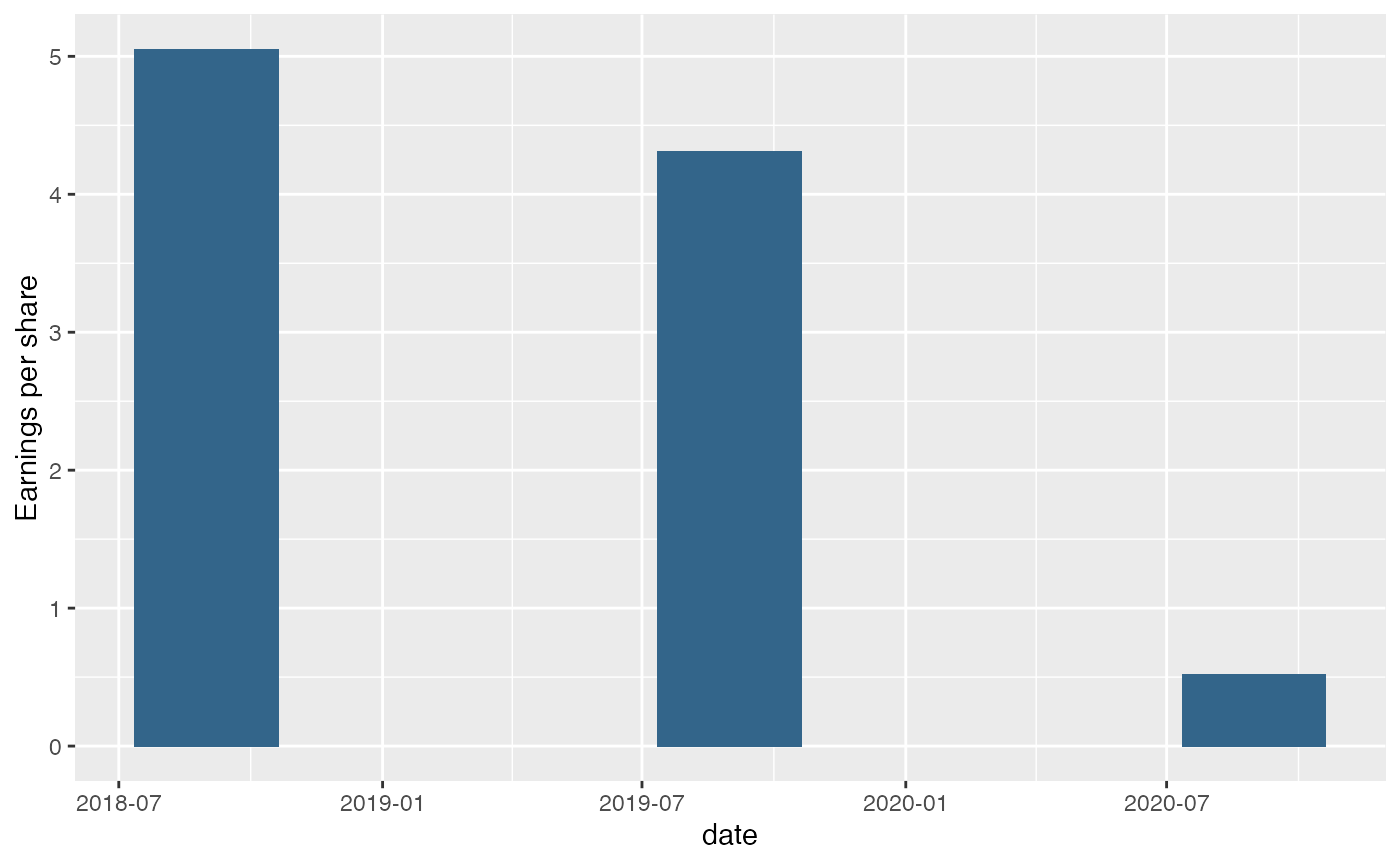
Return on invested capital > 9%
Return on invested capital will be calculated here as cash flow divided by equity + debt. Needs to be checked ⚠️.
roic <- fin$freeCashflow / (fin$longTermDebt + fin$totalStockholderEquity)
ggplot() +
geom_bar(aes(x = fin$endDate, y = roic), stat = "identity", fill = "#33658A", width = as.numeric(days(100))) +
xlab("date") + ylab("ROIC")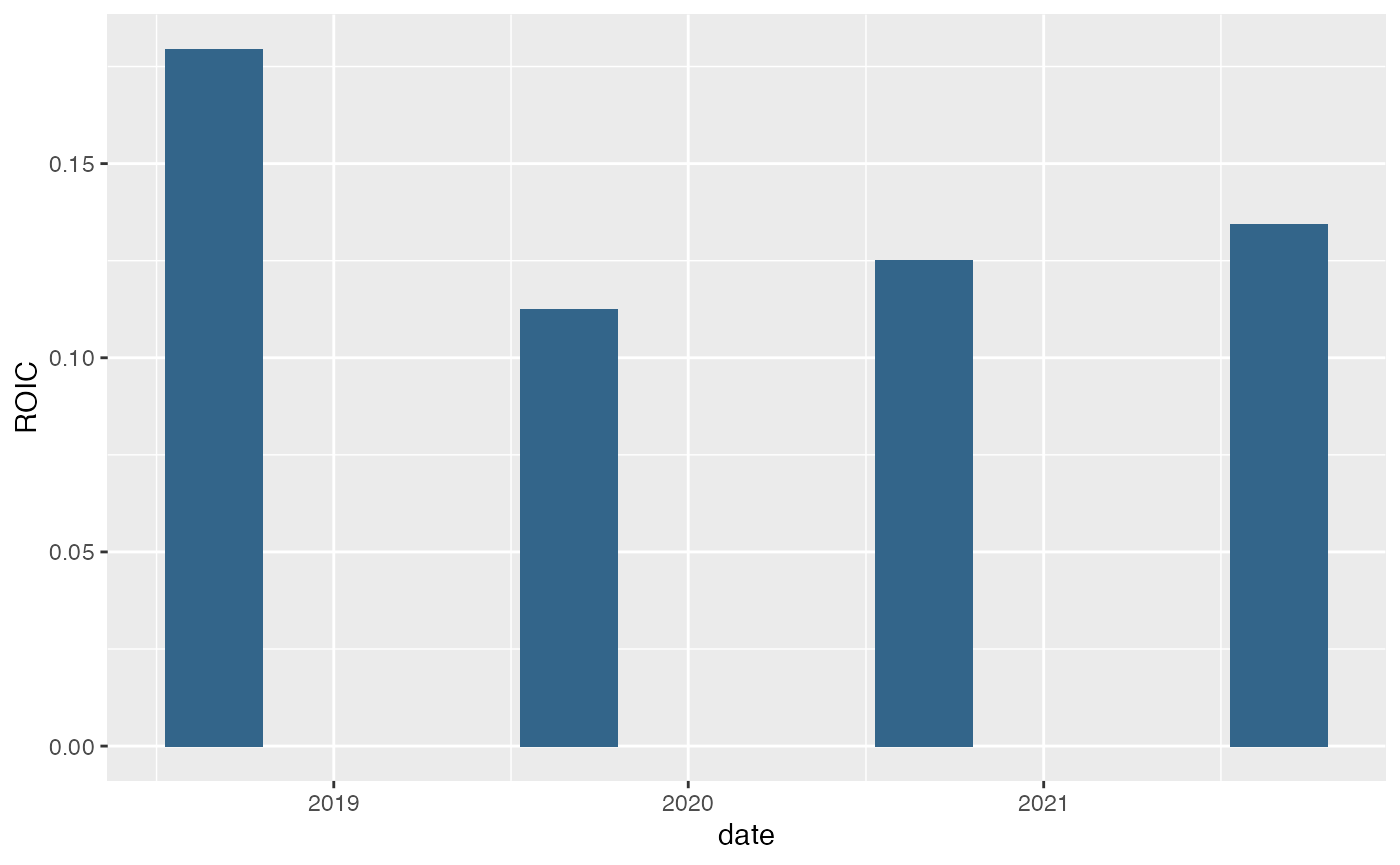
This gives us a mean ROIC of 0.14.
Revenue growth
Revenue should be going up, so let’s try a linear regression model.
##
## Call:
## lm(formula = fin$totalRevenue ~ fin$endDate)
##
## Residuals:
## 1 2 3 4
## 5.260e+09 -4.785e+09 -6.210e+09 5.735e+09
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.023e+11 1.752e+11 0.584 0.618
## fin$endDate 1.529e+01 1.106e+02 0.138 0.903
##
## Residual standard error: 7.811e+09 on 2 degrees of freedom
## Multiple R-squared: 0.009456, Adjusted R-squared: -0.4858
## F-statistic: 0.01909 on 1 and 2 DF, p-value: 0.9028
ggplot(fin) +
geom_point(aes(x = endDate, y = totalRevenue)) +
geom_abline(slope = coef(mod)[["fin$endDate"]], intercept = coef(mod)[["(Intercept)"]]) +
scale_y_continuous(expand = c(0.1, 0), limits = c(0, NA))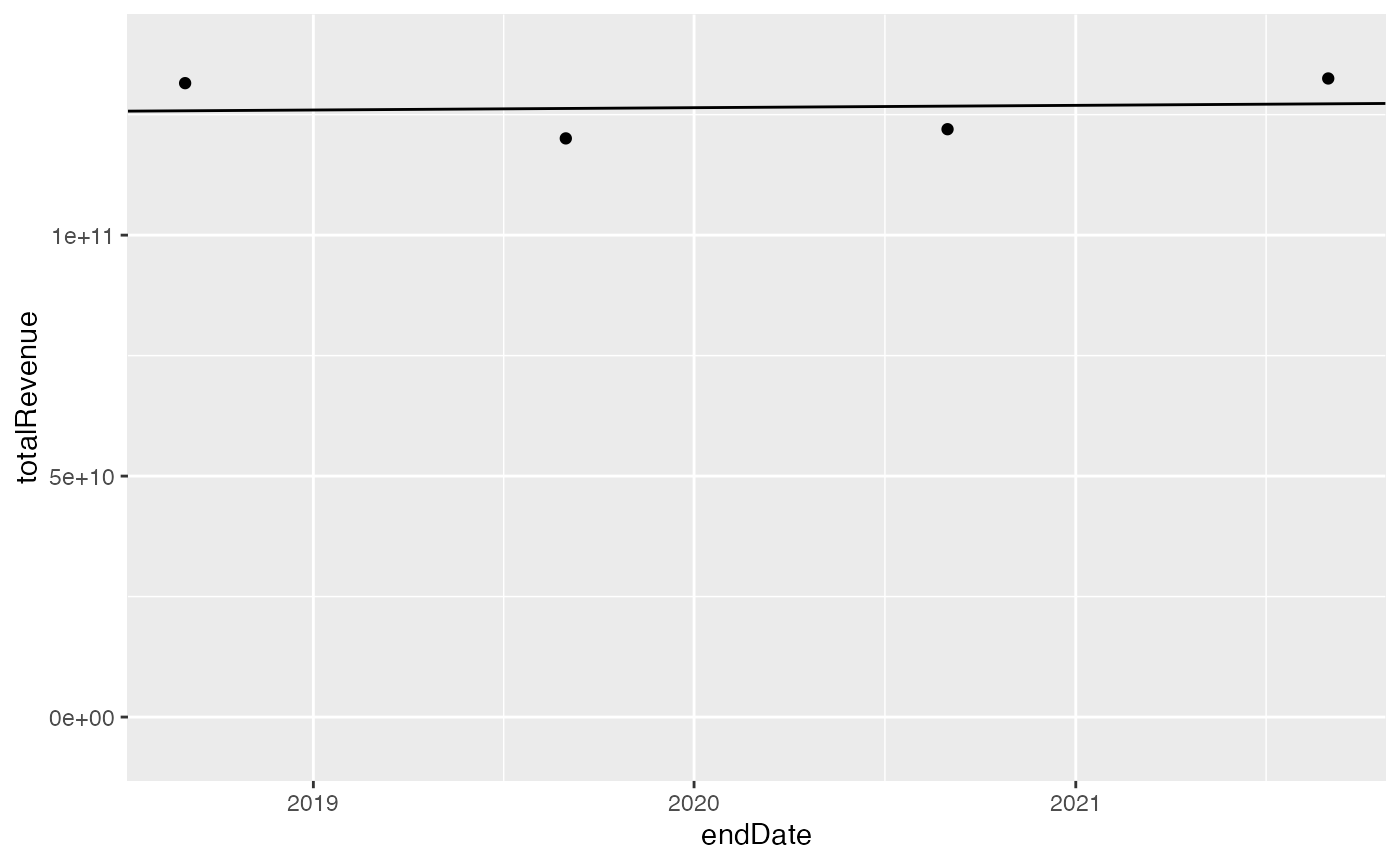
This gives us an annual growth rate of 0.
Net income growth
Same procedure as before:
##
## Call:
## lm(formula = fin$netIncome ~ fin$endDate)
##
## Residuals:
## 1 2 3 4
## 1.187e+09 -1.995e+09 4.313e+08 3.768e+08
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.804e+10 3.793e+10 1.530 0.266
## fin$endDate -3.477e+01 2.395e+01 -1.452 0.284
##
## Residual standard error: 1.691e+09 on 2 degrees of freedom
## Multiple R-squared: 0.513, Adjusted R-squared: 0.2695
## F-statistic: 2.107 on 1 and 2 DF, p-value: 0.2838
ggplot(fin) +
geom_point(aes(x = endDate, y = netIncome)) +
geom_abline(slope = coef(mod)[["fin$endDate"]], intercept = coef(mod)[["(Intercept)"]]) +
scale_y_continuous(expand = c(0.1, 0), limits = c(0, NA))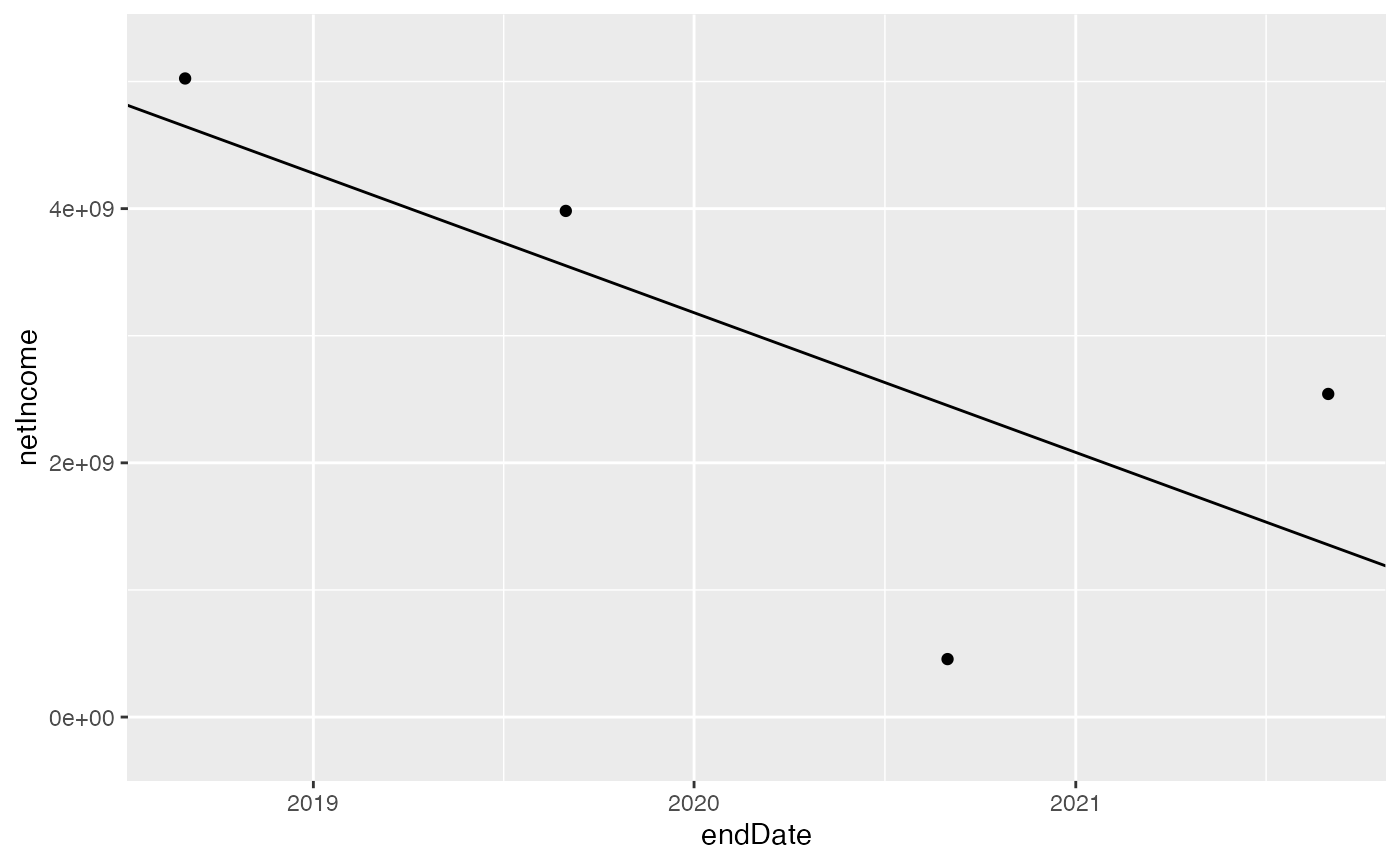
This gives us an annual growth rate of -0.37.
Shares outstanding
Shares outstanding should be decreasing or staying the same.
##
## Call:
## lm(formula = fin_web$dilutedAverageShares ~ fin_web$endDate)
##
## Residuals:
## 2 3 4
## 4736327 -9485630 4749303
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.779e+09 4.077e+08 9.268 0.0684 .
## fin_web$endDate -1.816e+00 2.601e-01 -6.981 0.0906 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11620000 on 1 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.9799, Adjusted R-squared: 0.9598
## F-statistic: 48.73 on 1 and 1 DF, p-value: 0.09058
ggplot(fin_web) +
geom_point(aes(x = endDate, y = dilutedAverageShares)) +
geom_abline(slope = coef(mod)[["fin_web$endDate"]], intercept = coef(mod)[["(Intercept)"]]) +
scale_y_continuous(expand = c(0.1, 0), limits = c(0, NA))
This gives us an annual growth rate of NA.
Free cash flow growth
##
## Call:
## lm(formula = fin$freeCashflow ~ fin$endDate)
##
## Residuals:
## 1 2 3 4
## 5.983e+08 -2.608e+08 -1.274e+09 9.367e+08
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.458e+10 2.713e+10 1.643 0.242
## fin$endDate -2.515e+01 1.714e+01 -1.468 0.280
##
## Residual standard error: 1.21e+09 on 2 degrees of freedom
## Multiple R-squared: 0.5185, Adjusted R-squared: 0.2778
## F-statistic: 2.154 on 1 and 2 DF, p-value: 0.2799
ggplot(fin) +
geom_point(aes(x = endDate, y = freeCashflow)) +
geom_abline(slope = coef(mod)[["fin$endDate"]], intercept = coef(mod)[["(Intercept)"]]) +
scale_y_continuous(expand = c(0.1, 0), limits = c(0, NA))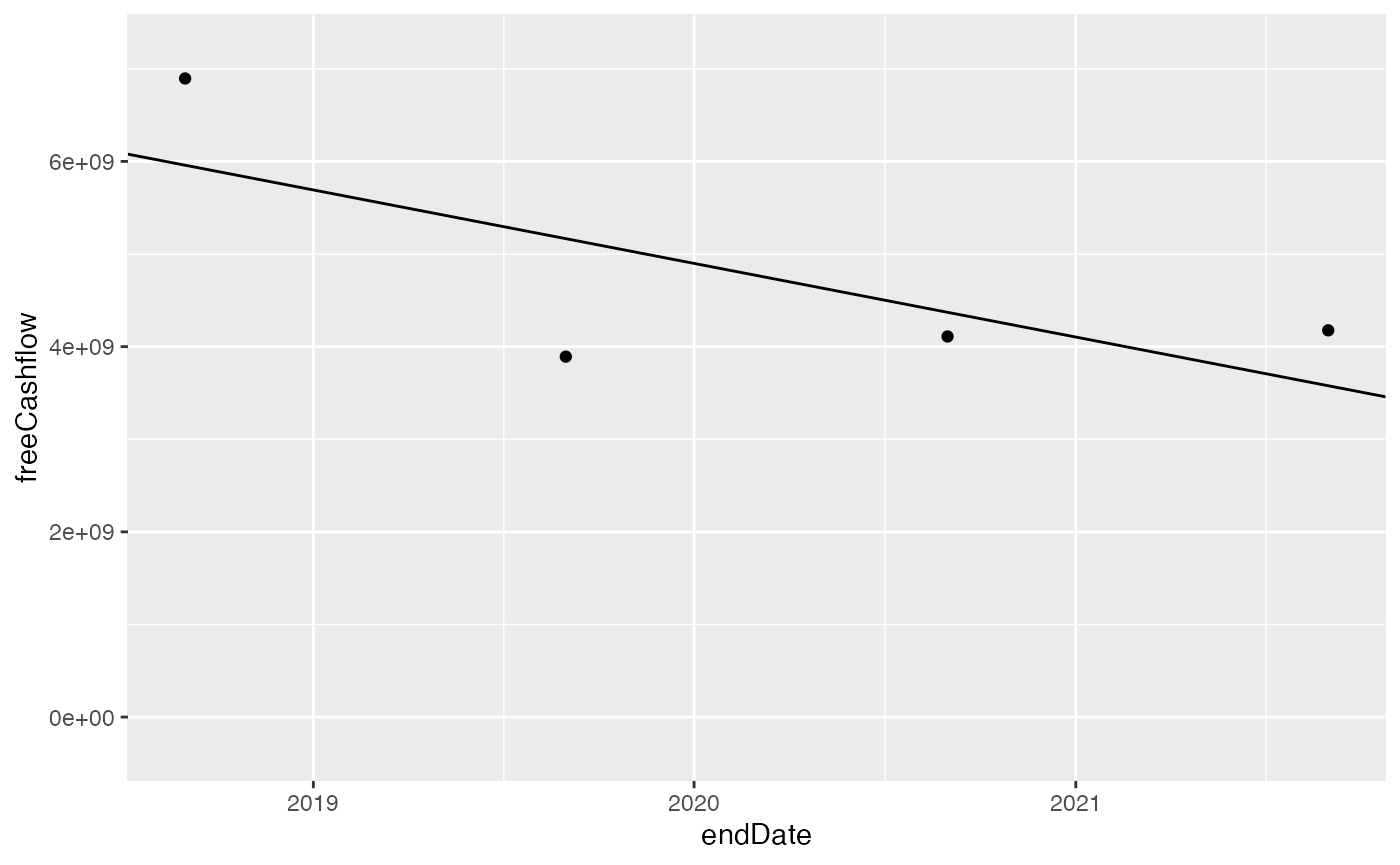
This gives us an annual growth rate of -0.17.
Price to free cash flow < 20
pfcf <- price$open / mean(fin$freeCashflow / fin_web$dilutedAverageShares, na.rm = TRUE)This gives us a price to free cash flow of 9.2.
ggplot() +
geom_bar(aes(x = fin$endDate, y = fin$freeCashflow / fin_web$dilutedAverageShares), stat = "identity", fill = "#33658A", width = as.numeric(days(100))) +
xlab("date") + ylab("Free cash flow per share")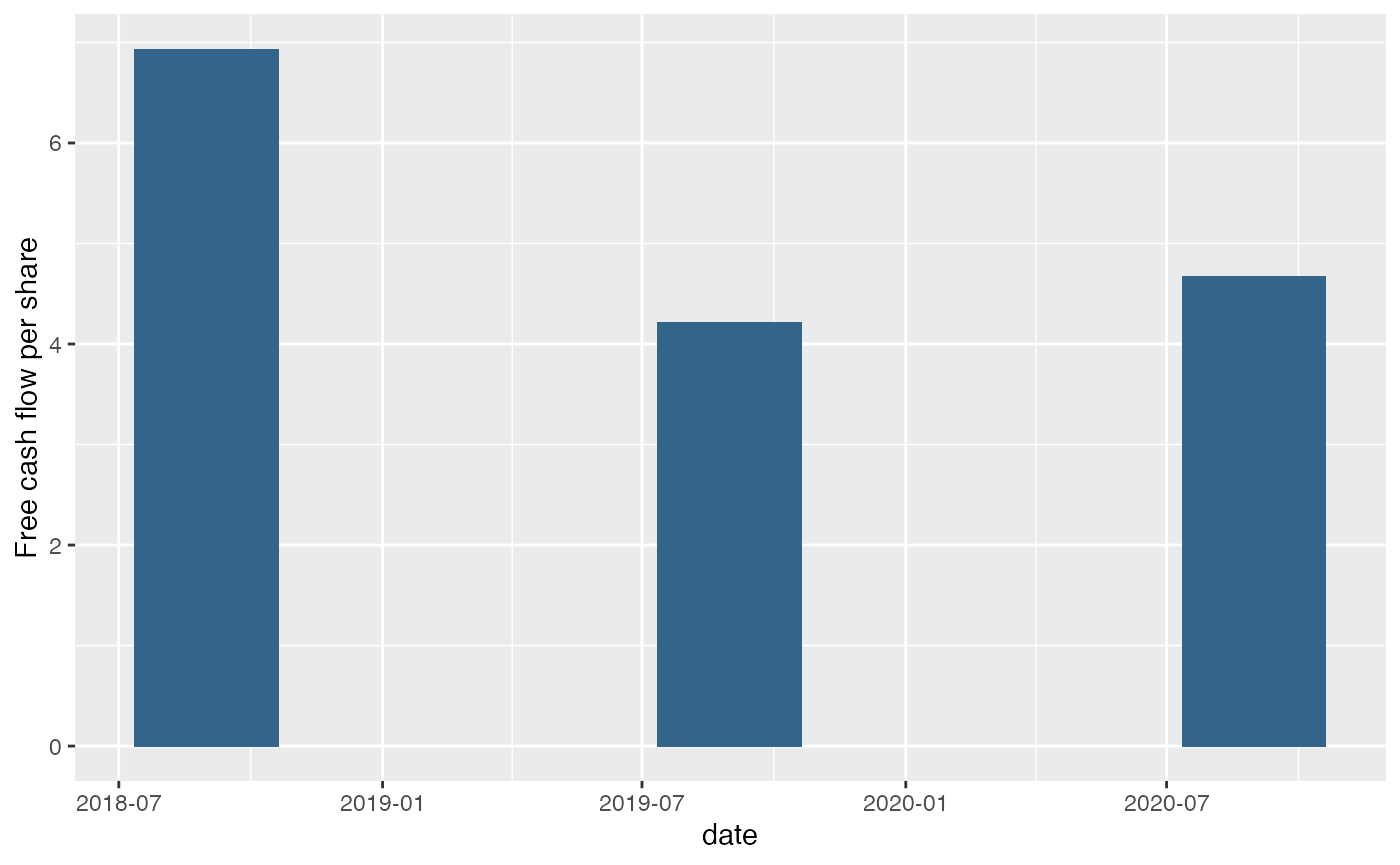
Bringing it all together
bind_rows(
eight_pillars("BBY"),
eight_pillars("MSFT")
)## # A tibble: 2 × 14
## pe_ratio pe_ratio_ok roic roic_ok revenue_growth revenue_growth_ok
## <dbl> <lgl> <dbl> <lgl> <dbl> <lgl>
## 1 19.4 TRUE 0.449 TRUE 0.0367 TRUE
## 2 63.9 FALSE 0.245 TRUE 0.139 TRUE
## # … with 8 more variables: net_income_growth <dbl>, net_income_growth_ok <lgl>,
## # shares_outstanding <dbl>, shares_outstanding_ok <lgl>, fcf_growth <dbl>,
## # fcf_growth_ok <lgl>, pfcf <dbl>, pfcf_ok <lgl>